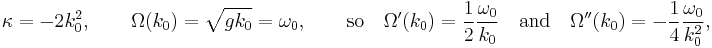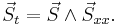Nonlinear Schrödinger equation
In theoretical physics, the nonlinear Schrödinger equation (NLS) is a nonlinear version of Schrödinger's equation. It is a classical field equation with applications to optics and water waves. Unlike the Schrödinger equation, it never describes the time evolution of a quantum state. It is an example of an integrable model.
In quantum mechanics, it is a special case of the nonlinear Schrödinger field, and when canonically quantized, it describes bosonic point particles with delta-function interactions — the particles either repel or attract when they are at the same point. The nonlinear Schrödinger equation is integrable when the particles move in one dimension of space. In the limit of infinite strength repulsion, the nonlinear Schrödinger equation bosons are equivalent to one dimensional free fermions.
Contents |
The equation
The nonlinear Schrödinger equation is the partial differential equation[1]
for the complex field ψ(x,t).
This equation arises from the Hamiltonian[1]
with the Poisson brackets
Quantum version
To get the quantized version, simply replace the Poisson brackets by commutators
and normal order the Hamiltonian
The quantum version was solved by Bethe ansatz by Lieb and Liniger . Thermodynamics was described by Chen Nin Yang. Quantum correlation functions also were evaluated, see.[2] The model has higher conservation laws, expression in terms of local fields can be found in. [1].
Solving the equation
The nonlinear Schrödinger equation is integrable: It can be solved with the inverse scattering transform. The corresponding linear system of equations is known as the Zakharov–Shabat system:
where
The nonlinear Schrödinger equation arises as compatibility condition of the Zakharov–Shabat system:
By setting 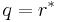 or
or 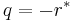 the nonlinear Schrödinger equation with attractive or repulsive interaction is obtained.
the nonlinear Schrödinger equation with attractive or repulsive interaction is obtained.
An alternative approach uses the Zakharov–Shabat system directly and employs the following Darboux transformation:
which leaves the system invariant.
Here, 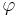 is another invertible matrix solution (different from
is another invertible matrix solution (different from 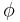 ) of the Zakharov–Shabat system with spectral parameter
) of the Zakharov–Shabat system with spectral parameter  :
:
Starting from the trivial solution 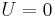 and iterating, one obtains the solutions with n solitons.
and iterating, one obtains the solutions with n solitons.
Computational solutions are found using a variety of methods, like the split-step method.
Galilean invariance
The nonlinear Schrödinger equation is Galilean invariant in the following sense:
Given a solution 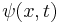 a new solution can be obtained by replacing
a new solution can be obtained by replacing 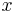 with
with 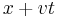 everywhere in
everywhere in 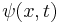 and by appending a phase factor of
and by appending a phase factor of 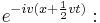
The nonlinear Schrödinger equation in fiber optics
In optics, the nonlinear Schrödinger equation occurs in the Manakov system, a model of wave propagation in fiber optics. The function  represents a wave and the nonlinear Schrödinger equation describes the propagation of the wave through a nonlinear medium. The second-order derivative represents the dispersion, while the κ term represents the nonlinearity. The equation models many nonlinearity effects in a fiber, including but not limited to self-phase modulation, four-wave mixing, second harmonic generation, stimulated Raman scattering, etc.
represents a wave and the nonlinear Schrödinger equation describes the propagation of the wave through a nonlinear medium. The second-order derivative represents the dispersion, while the κ term represents the nonlinearity. The equation models many nonlinearity effects in a fiber, including but not limited to self-phase modulation, four-wave mixing, second harmonic generation, stimulated Raman scattering, etc.
The nonlinear Schrödinger equation in water waves
For water waves, the nonlinear Schrödinger equation describes the evolution of the envelope of modulated wave groups. In a paper in 1968, Vladimir E. Zakharov describes the Hamiltonian structure of water waves. In the same paper Zakharov shows, that for slowly-modulated wave groups, the wave amplitude satisfies the nonlinear Schrödinger equation, approximately. The value of the nonlinearity parameter к depends on the relative water depth. For deep water, with the water depth large compared to the wave length of the water waves, к is negative and envelope solitons may occur.
For shallow water, with wavelengths longer than 4.6 times the water depth, the nonlinearity parameter к is positive and wave groups with envelope solitons do not exist. Note, that in shallow water surface-elevation solitons or waves of translation do exist, but they are not governed by the nonlinear Schrödinger equation.
The nonlinear Schrödinger equation is thought to be important for explaining the formation of rogue waves.
The complex field ψ, as appearing in the nonlinear Schrödinger equation, is related to the amplitude and phase of the water waves. Consider a slowly-modulated carrier wave with water surface elevation η of the form:
where a( x0 , t0 ) and θ( x0 , t0 ) are the slowly-modulated amplitude and phase. Further ω0 and k0 are the (constant) angular frequency and wavenumber of the carrier waves, which have to satisfy the dispersion relation ω0 = Ω( k0 ). Then
So its modulus |ψ| is the wave amplitude a, and its argument arg(ψ) is the phase θ. The relation between the physical coordinates ( x0 , t0 ) and the ( x , t ) coordinates, as used in the nonlinear Schrödinger equation given above, is given by:
Thus ( x, t ) is a transformed coordinate system moving with the group velocity Ω'( k0 ) of the carrier waves, The dispersion-relation curvature Ω"( k0 ) is always negative for water waves under the action of gravity.
For waves on the water surface of deep water, the coefficients of importance for the nonlinear Schrödinger equation are:
with g the acceleration by gravity.
Gauge equivalent counterpart
NLSE (1) is gauge equivalent to the following isotropic Landau-Lifshitz equation (LLE) or Heisenberg ferromagnet equation
Note that this equation admits several integrable and non-integrable generalizations in 2+1 dimensions like the Ishimori equation and so on.
See also
- Phi to the fourth for a related model in quantum field theory
- Mathematical aspects of the nonlinear Schrödinger equation, on Dispersive Wiki
References
- ^ a b V.E. Zakharov; S.V. Manakov (1974). "On the complete integrability of a nonlinear Schrödinger equation". Journal of Theoretical and Mathematical Physics 19 (3): 551–559. Bibcode 1974TMP....19..551Z. doi:10.1007/BF01035568 Originally in: Teoreticheskaya i Matematicheskaya Fizika 19 (3): 332–343. June, 1974
- ^ Korepin, V. E.; Bogoliubov N. M., Izergin, A. E. (1993). Quantum Inverse Scattering Method and Correlation Functions. Cambridge University Press,. ISBN 9780521586467.
External links
- Nonlinear Schrodinger Equation with a Cubic Nonlinearity at EqWorld: The World of Mathematical Equations.
- Nonlinear Schrodinger Equation with a Power-Law Nonlinearity at EqWorld: The World of Mathematical Equations.
- Nonlinear Schrodinger Equation of General Form at EqWorld: The World of Mathematical Equations.
- V. E. Zakharov (1968). "Stability of periodic waves of finite amplitude on the surface of a deep fluid". Journal of Applied Mechanics and Technical Physics 9 (2): 190–194. Bibcode 1968JAMTP...9..190Z. doi:10.1007/BF00913182. Originally in: Zhurnal Prikdadnoi Mekhaniki i Tekhnicheskoi Fiziki 9 (2): 86–94, 1968.
- Fluid Mechanics by Falkovich, Section 3.3
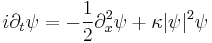
![H=\int dx \left[{1\over 2}|\partial_x\psi|^2%2B{\kappa \over 2}|\psi|^4\right]](/2012-wikipedia_en_all_nopic_01_2012/I/7c911a29de7398645238d2bcb6d94ff8.png)
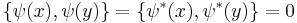
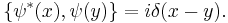
![[\psi(x),\psi(y)]=[\psi^*(x),\psi^*(y)]=0\,](/2012-wikipedia_en_all_nopic_01_2012/I/1ed9034203f347093e0d959810cc2516.png)
![[\psi^*(x),\psi(y)]=-\delta(x-y)\,](/2012-wikipedia_en_all_nopic_01_2012/I/c34aa395821abe3e4983a5cf03902350.png)
![H=\int dx \left[{1\over 2}\partial_x\psi^\dagger\partial_x\psi%2B{\kappa \over 2}\psi^\dagger\psi^\dagger\psi\psi\right].](/2012-wikipedia_en_all_nopic_01_2012/I/8f08f4331a99d8e4326499e5b20ffb27.png)
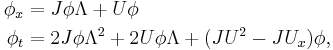
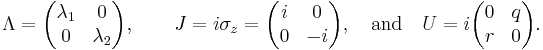
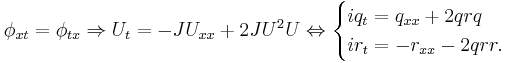
![\begin{align}
& \phi \to \phi[1]=\phi\Lambda-\sigma\phi \\
& U \to U[1]=U%2B[J,\sigma] \\
& \sigma = \varphi\Omega\varphi^{-1}
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/38d94ceec6b6b941a13fbadb5312a9ef.png)
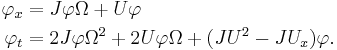
![\psi(x,t) \mapsto \psi_{[v]}(x,t)=\psi(x%2Bvt,t)\; e^{-iv(x%2B\frac{1}{2}vt)}.](/2012-wikipedia_en_all_nopic_01_2012/I/41ae05d23b29f7403f5d89fafa2b6661.png)
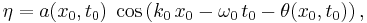
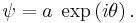
![x = k_0 \left[ x_0 - \Omega'(k_0)\; t_0 \right]
\qquad \text{ and } \qquad
t = k_0^2 \left[ -\Omega''(k_0) \right]\; t_0.](/2012-wikipedia_en_all_nopic_01_2012/I/9274d8ed8112fa9c6d2c35bf6f3d82e0.png)